1
「チャート式」ならぬ「チート式」を作りました。
正攻法とチート解法（裏技、セコ技、邪道、大学数学によるオーバーキル等）を比較・解説します。
以前大学院レベルの「チェート式」をあげた際に来た「俺はむしろチート式が見たい」というご要望にお応えしました。
#チャート式 #チート式 #チェート式
2
算数のチート式を作りました。
お題は以前中受界隈が難しすぎるぞと騒ついた「1/9998の小数第96位」を求めさせる開成の過去問で、正攻法では筆算の原理から規則性を見出す必要がある上に2重にひっかけがあります。
そんな開成中学の算数の超難問をマクローリン展開でフルボッコにします。
#チート式
3
今回のチートはみんな大好き円周率の近似についてです。
東大のπ>3.05や阪大挑戦枠の3.141#チート式
4
#チート式 っぽい話ですが、高次式が2次式で割り切れる条件を求める方法は色々あり、計算量が違います。
エスパーなら答えを予言してから答えの一意存在を示すのが最速です。
今回は答えがたまたま(っていうのは嘘で仕組みましたが)進次郎のシルエット数46になるので小泉進次郎風にまとめました。
5
今回のチート式は留数計算です。
(いつかやると思ってたという声が聞こえてきそうです)
高校数学では凄まじいエネルギーを消費する必殺技しか通用しない高難度の積分ですが、留数定理を使えば“積分すらせずに”積分の値が求まります。
これが複素解析の力です。
#チート式
6
数III以外のチートも見たいという意見が多かったので数IIのチートを考えました。
お題は記述でも堂々と使える二重接線を瞬時に求める式変形テクと、記述では使わない方がいいけど検算で役立つ1/30公式等の一般化。
受験期真っ只中でもきちんとTwitterを見ている良い子の皆さんへプレゼント！
#チート式
7
8
ついに禁断の「黒チート」を解禁する時が来ました。
東大の過去問を例にして、n個のサイコロの出た目の和や積が与えられた条件を満たす値になる確率や場合の数を「代数的」に計算できる裏技公式を紹介します。
場合の数を多項式の係数と見れば、面倒な場合分けは不要になります。
#チート式
9
今回のチート式は5乗の和の公式をできるだけ効率よく導出します。高校数学では3乗和まで暗記させられて4乗和がよく問題で出されますが、5乗以上は正攻法では計算が地獄になります。
後で思いついたのですが、チート④としてf(x)=x^5にEuler–Maclaurinの和公式を適用しても簡単に求まります。
#チート式
10
前回のチート式では「脱法ロピタル」が好評だったので「脱法パップスギュルダン」も作ってみました。記述も計算も楽です。この手法はあまり知られていないと思います。
重心の定義からパップスギュルダンの定理とほぼ等価ですが、有名な裏技であるバウムクーヘン積分はより広範に使えます。
#チート式
11
積分アレルギーのある人から「積分のチートばっかりだ」とクレームが入ったので積分と関係ないチートを考えました。
対称性・交代性を上手く使えば、面倒な文字式の計算を全くせずに因数分解できます。
対称性や交代性がない式の因数分解も多変数の因数定理で楽にできる場合もあります。
#チート式
12
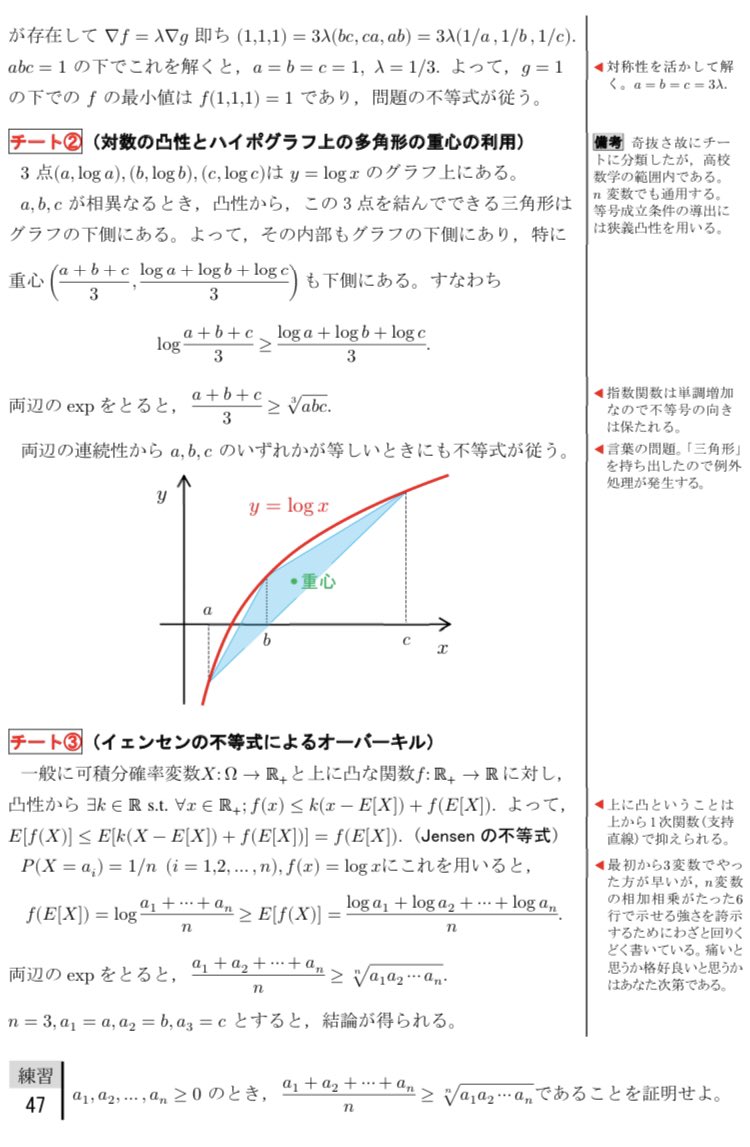
多変数の相加平均・相乗平均の関係は高校数学では2^n変数の場合を先に示す独特の帰納法やゴリゴリ計算で導かれることが多いですが、測度論や凸性を使うとほぼ何の計算もせず一瞬で導けます。
他にも代表的な斉次性の利用やラグランジュの未定乗数法など計7通りの証明を紹介します。
#チート式
