101
「去年の別の講義と半分くらい内容かぶってます。真面目な人は新しいこと教えてほしいでしょうが、同じこと勉強して単位を2倍もらえてラッキーだと思う人もいるでしょう」
「ICT-LMなんとか」
「UTASはあまり信用できないので」
「皆さん僕の顔なんか見たくもないと思うのでビデオは常にオフにします」
102
級数の収束判定法としてコーシーの判定法、ダランベールの判定法、ラーべの判定法、ガウスの判定法、クンマーの判定法など、強力なものが沢山知られていますが、いずれも完全無欠ではありません。
Flint Hills級数と呼ばれる、こんな単純な形なのに収束するか発散するかさえ未解決の級数があります。
103
「まるちゃん、選択公理を無意識に仮定するのはやめなよ。あと、標数を確認せずに2とか3で割るのもやめよう。それと、勝手に作った集合から元をとるときは空じゃないか確認しなよ。limsupの計算とかεδ論法に基づかずに直感で極限をとるのもよくないよ。ついでにlimと∫を勝手に交換するのもやめなよ」
104
前者は数学徒、後者は物理学徒にウケやすい。数学徒は写像や定義域を気にするのに対し、物理学徒は量(実体)やイメージを気にする。前者は「代入する量y,y'が独立じゃなくても座標変数w,vは独立だから偏微分できる」という話だが、後者はその微分の正当化が終わった後で量δy,δy'の従属性を処理する話で
105
色々な「場合の数」の母関数を挙げてみました。組合せ論的な情報が代数・解析的に扱えるようになるのが面白いです。機械的に場合の数が求まります。直接一般項を出す方が早い場合も多いですが、漸化式等から代数方程式・微分方程式を作って母関数を求め、母関数から一般項も求まります。
106
「正∞角形は円である」あるいは「lim[n→∞]正n角形は円である」という根拠を7つ挙げてみました。
初等幾何はもちろん、集合論、位相空間論、測度論、関数解析学など、様々な観点から色々と分析できます。
107
悟空語で数学してみました。
お題はディリクレ積分の一般化です。
∫[0,∞](sin(x))^n /x^β dx (n: 自然数, β: 複素数, Re β≧1)の値(あてぇ)を求めます(求めっぞ)。
複素けぇ析のつえぇ定理の力でディリクレ積分がどんだけパワーアップすっか、オラわくわくすっぞ！
ぜってぇ見てくれよな！
108
チェザロ平均の収束は「ε-N論法を使わなければ証明できない例」としてよく挙げられますが、これは嘘で、実は高校範囲内で示せます。
limと∫の順序交換も測度論なしで高校範囲内で展開できます。
中間値の定理が実数の連続性と等価なので、実は原理的にε-δ論法自体も高校数学から逆に「導出」できます
109
今年の東大入試理系数学のうち骨がありそうな問題を一般化してみました。
なんか難化したとか言われていますが、それよりも難しくしたので東大を超えたい人は是非挑戦してみてください。
一般化すると本質が可視化され、問題がいかに練られていたかもよく分かるようになります。
111
高校生は無意識に"原点を通らない"グラフを想像して「原点で0じゃない」という表現に違和感を覚えるみたいですが、大学で数学や物理を学んだ人は無意識に高次元への一般化を想像してx=0を実1次元空間ℝあるいは複素数平面ℂの原点だと思ってそこで関数値が0でないと考えるので自然に感じるらしいです。
112
ㅤ
₍₍⁽⁽sin(nx)₎₎⁾⁾
見て！sin(nx)が踊って(振動して)いるよ
かわいいね
⁽⁽₍₍⁽⁽sin(nx)₎₎⁾⁾₎₎
nが大きくなると踊りが激しくなるよ
めっちゃ可愛い
D’-lim sin(nx)=0
超関数と見做されたsin(nx)は0に収束し、踊るのをやめてしまいました
リーマンルベーグの定理のせいです
113
もしもベッセル関数を扱うチャート式があったら。
ベッセル関数は実は数学科では習いませんが、物理・工学系では三角関数と同じくらい湯水のように使われます。
級数展開、漸化式、直交関係、母関数、加法公式、積分表示、漸近公式、グラフ、J_{1/2}の表示公式等は演習問題で頻出です。
#チェート式
114
ルベーグ可積分ではない（従ってリーマン可積分でもない）が、ヘンストック・クルツヴァイル可積分な関数の例。
ルベーグ積分は「万能」と言えるかもしれませんが、「全能」ではありません。
115
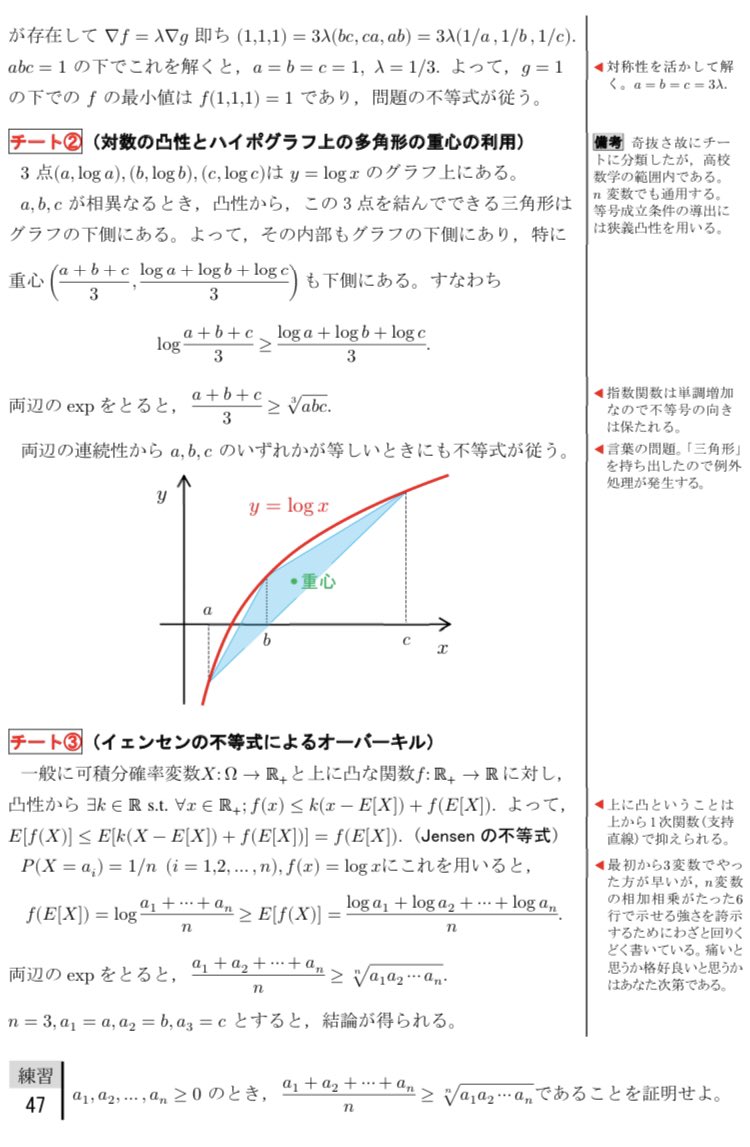
多変数の相加平均・相乗平均の関係は高校数学では2^n変数の場合を先に示す独特の帰納法やゴリゴリ計算で導かれることが多いですが、測度論や凸性を使うとほぼ何の計算もせず一瞬で導けます。
他にも代表的な斉次性の利用やラグランジュの未定乗数法など計7通りの証明を紹介します。
#チート式
117
ロピタる：ロピタルの定理を使う
ピタゴラす：直角三角形の辺の長さを求める
ブラーマグプった：円に内接する四角形の面積を4辺の長さから求めた
ルベーぐ：測度で積分する
エラトステネす：数を篩にかけて素数だけ残す
ガウす：7歳で等差数列の和の公式に気付く
メビウす：どっちが表か分からなくなる
118
「正則と言えば？」
線形代数学徒「正則行列」
複素解析学徒「正則関数」
位相空間論徒「正則空間」
線形表現論徒「正則表現」
グラフ理論徒「正則グラフ」
公理的集合論徒「正則性公理」
文系「『まさのり』って誰？」
120
ラプラシアンの固有値と固有関数について数年前に個人的にまとめたメモです。こういう一覧表がネットに無かったので自分で作りました。
元々個人用なので汚い上に一部の数理物理学徒と楕円型偏微分方程式論徒にしかウケないと思いますが、誰にも見せないでお蔵入りになるのは勿体無いので公開します。
121
その年の日本の全大学の数学の入試問題の中で最難とされる伝説の2019年度東工大入試問題第4問（空間をn個の平面で分割したときにできる領域の個数に関する問題）の4次元バージョンを作ってみました。解答も付けておきます。
次元が上がってるので元ネタより遥かに難しいです。死ぬほど難しいです。
122
全ての階数の微分と積分(積分定数は平均が0になるように選ぶ)が一様に有界な実関数は本質的に三角関数しかないらしい。
しかもこの条件だけで周期が定数倍の違いもなくちょうど2πに決まってしまうのが驚き。
123
流石に「人は区別するが、同じ色の玉は区別しない」は暗黙の了解で但し書きされないけど、これも解釈に依りそう。
例えば「7人を円形に並べる方法は何通りか」と問われたら普通は(7-1)!=720通りだけど、人間が肉の塊にしか見えない重度のサイコパスや宇宙人は人間が区別できないから1通りって答える。
124
幾何学Iの先生の悪行
・板書が速すぎる
・「昔はもっと速くできた」「中学レベルかな」等とイキる
・みんな圏論を既知だと勘違いする
・まだ代数で習ってない代数の概念を平然と多用する
・レンズ空間
・普通は学部で習わない固有不連続作用を自分の趣味で重要と位置付ける
・演習を院試より難しくする
125
暇人かつ数学徒ならみんなやると思いますが、円と楕円（内部を含む）の方程式だけを使って「いのちの輝き」を描きました。
全部で16個の数式を使っていますが、それらをmin関数でつなぎ合わせれば全体を1つの数式で表すこともできます。
東大数理←東大数学科←理科I類←国高68th800。学生です。数学垢。5日に1回浮上。大学数学耐性のない人はフォロー非推奨。#チート式 の作者。関数解析が好き。リツイートが嫌なら「リツイートのみ非表示」に設定してください。