126
色々な「場合の数」の母関数を挙げてみました。組合せ論的な情報が代数・解析的に扱えるようになるのが面白いです。機械的に場合の数が求まります。直接一般項を出す方が早い場合も多いですが、漸化式等から代数方程式・微分方程式を作って母関数を求め、母関数から一般項も求まります。
128
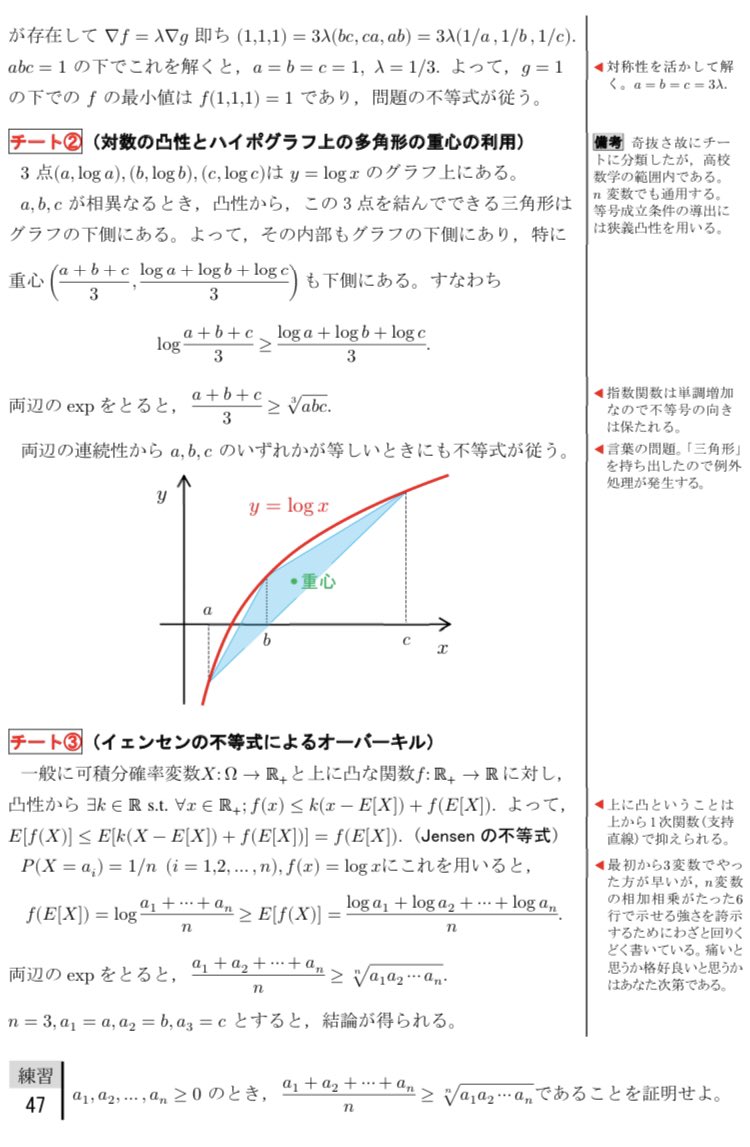
多変数の相加平均・相乗平均の関係は高校数学では2^n変数の場合を先に示す独特の帰納法やゴリゴリ計算で導かれることが多いですが、測度論や凸性を使うとほぼ何の計算もせず一瞬で導けます。
他にも代表的な斉次性の利用やラグランジュの未定乗数法など計7通りの証明を紹介します。
#チート式
131
「◯◯積分」という言葉を集めました。200個以上あります。
数学のみならず物理も混ざってます。
積分って200種類あんねん。
132
今回のチート式は留数計算です。
(いつかやると思ってたという声が聞こえてきそうです)
高校数学では凄まじいエネルギーを消費する必殺技しか通用しない高難度の積分ですが、留数定理を使えば“積分すらせずに”積分の値が求まります。
これが複素解析の力です。
#チート式
133
4つ以上の集合のベン図は描くだけでも至難の業。
円だけで表現可能なのは3集合までで、4,5集合だと楕円くらいは必要になり、6集合以上だと更にぐにゃぐにゃの図形が必要になる。
回転対称性をもつベン図は11集合まで知られてるけど実用性は皆無。
procrasist.com/entry/venn-dia…
visualizing.jp/euler-venn-dia…
134
チェザロ平均の収束は「ε-N論法を使わなければ証明できない例」としてよく挙げられますが、これは嘘で、実は高校範囲内で示せます。
limと∫の順序交換も測度論なしで高校範囲内で展開できます。
中間値の定理が実数の連続性と等価なので、実は原理的にε-δ論法自体も高校数学から逆に「導出」できます
135
東大「π>3.05を示せ」
阪大挑戦枠「π>3.141を示せ」
ワイ大学「π>3.14159265358979323を示せ」
#円周率の日
136
数学で計画性をもたずにめちゃくちゃに添字を付けていくと、こんな感じの地獄になります。
137
「実数は存在するが、虚数は存在しない」と言う人vs「虚数が存在しないなら実数も存在しない」と言う人
138
円を使った「相加平均≧相乗平均」の図解は割と有名ですが、実はそれだけではなく「最大値≧二乗平均平方根(RMS)≧相加平均≧相乗平均≧調和平均≧最小値」という6つのヘルダー平均(一般化平均)の関係が1つの半円だけで視覚化できます。更にこれを動かせば等号成立条件も分かります。
139
全ての階数の微分と積分(積分定数は平均が0になるように選ぶ)が一様に有界な実関数は本質的に三角関数しかないらしい。
しかもこの条件だけで周期が定数倍の違いもなくちょうど2πに決まってしまうのが驚き。
東大数理←東大数学科←理科I類←国高68th800。学生です。数学垢。5日に1回浮上。大学数学耐性のない人はフォロー非推奨。#チート式 の作者。関数解析が好き。リツイートが嫌なら「リツイートのみ非表示」に設定してください。