51
52
53
位相が強まると、部分集合が開・閉になりやすくなり、稠密になりにくくなり、閉包が小さくなり、点列が収束しにくくなり、その空間を始域とする写像が連続になりやすくなり、終域とする写像が連続になりにくくなり、分離性が良くなり(従ってハウスドルフになりやすくなり)、コンパクト性が悪くなる。
54
積分アレルギーのある人から「積分のチートばっかりだ」とクレームが入ったので積分と関係ないチートを考えました。
対称性・交代性を上手く使えば、面倒な文字式の計算を全くせずに因数分解できます。
対称性や交代性がない式の因数分解も多変数の因数定理で楽にできる場合もあります。
#チート式
55
57
人知を超越するほど頭の悪い人の2021年度東大数学第4問の解き方 twitter.com/keisankionwyki…
58
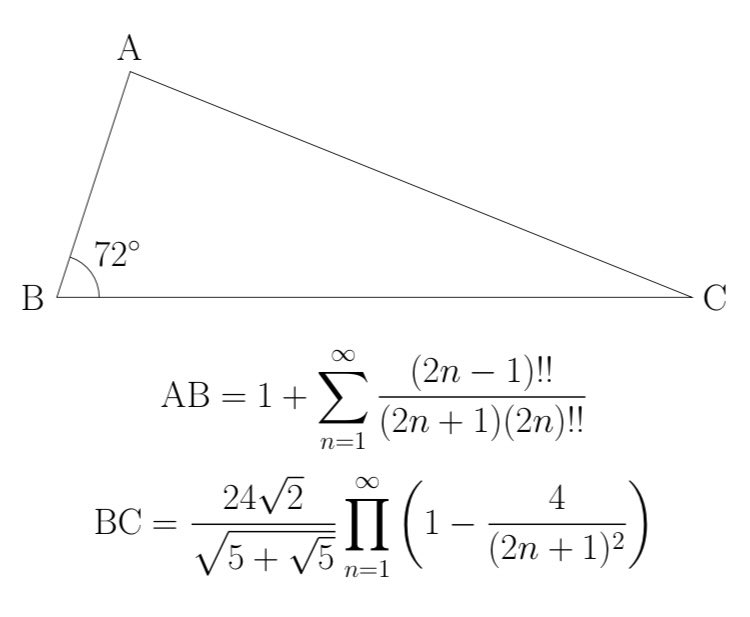
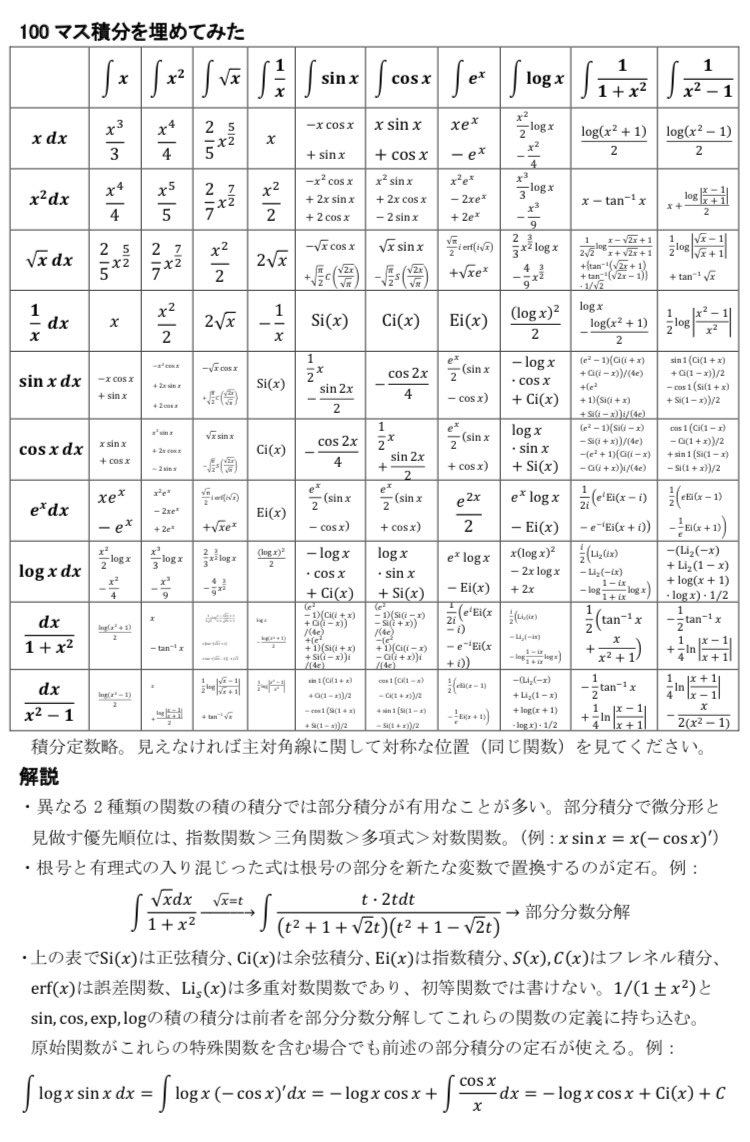
円周率の日なので面積がπになるいびつな三角形を作ってみました。
#円周率の日
59
実際に数式で使ったら便利そうな部首を定義してみました。 twitter.com/Keyneqq/status…
61
62
63
64
「1からnまでの数字が書かれたn枚のカードがある」と書くと普通は1枚に1つずつ数字が書かれてると思うけど、ごく稀に不合格者が「1枚に1からnまでの数字が全部書いてあると思った」とクレームつけてくるから入試問題を作る際は細心の注意を払って誤解の余地がない問題文を作るって恩師が仰ってた
65
流石に「人は区別するが、同じ色の玉は区別しない」は暗黙の了解で但し書きされないけど、これも解釈に依りそう。
例えば「7人を円形に並べる方法は何通りか」と問われたら普通は(7-1)!=720通りだけど、人間が肉の塊にしか見えない重度のサイコパスや宇宙人は人間が区別できないから1通りって答える。
66
67
69
70
#チート式 っぽい話ですが、高次式が2次式で割り切れる条件を求める方法は色々あり、計算量が違います。
エスパーなら答えを予言してから答えの一意存在を示すのが最速です。
今回は答えがたまたま(っていうのは嘘で仕組みましたが)進次郎のシルエット数46になるので小泉進次郎風にまとめました。
71
文系「三角関数は社会で役に立たない」
理系「測量、建築、地図製作、画像・音声処理、ゲーム制作、航海、航空、医療、教育、美術、振動工学、電子工学、制御工学、情報工学、統計、機械学習、物理、宇宙開発、軍事、交通、防災、気象予報、発電、通信等、電気・波・情報・図形が関わる全てに不可欠」
72
鋭い文系「三角関数が社会で役に立つ様子を私が想像できないのは、実際に役立たないからじゃなくて、三角関数を使わなくてもいい生き方を私が選択したからに過ぎないんだろうな。私が三角関数を使わなくても現代人として生きられるのは、代わりに三角関数を使ってくれる理工系がいるお陰なんだろうな」
73
鋭い理系「古文が社会で役に立つ様子を私が想像できないのは、実際に役立たないからじゃなくて、古文を使わなくていい生き方を私が選択したからに過ぎない。私が古文を使わなくて済む現在は、文系が古文・漢文に秘められた文化と先人の叡智を分析して現代社会に至る歴史を形作ったお陰なんだろうな」
74
75
算数のチート式を作りました。
お題は以前中受界隈が難しすぎるぞと騒ついた「1/9998の小数第96位」を求めさせる開成の過去問で、正攻法では筆算の原理から規則性を見出す必要がある上に2重にひっかけがあります。
そんな開成中学の算数の超難問をマクローリン展開でフルボッコにします。
#チート式