76
「1からnまでの数字が書かれたn枚のカードがある」と書くと普通は1枚に1つずつ数字が書かれてると思うけど、ごく稀に不合格者が「1枚に1からnまでの数字が全部書いてあると思った」とクレームつけてくるから入試問題を作る際は細心の注意を払って誤解の余地がない問題文を作るって恩師が仰ってた
77
78
79
81
実際に数式で使ったら便利そうな部首を定義してみました。 twitter.com/Keyneqq/status…
82
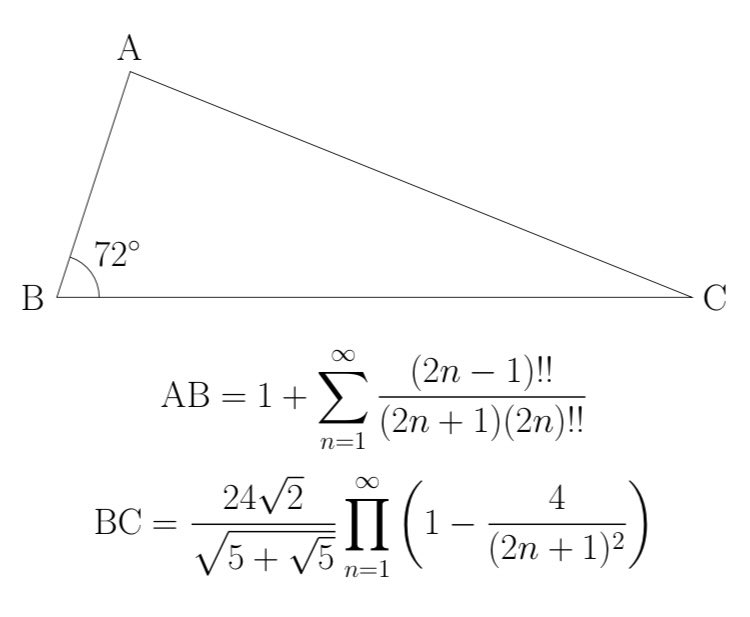
円周率の日なので面積がπになるいびつな三角形を作ってみました。
#円周率の日
83
人知を超越するほど頭の悪い人の2021年度東大数学第4問の解き方 twitter.com/keisankionwyki…
85
86
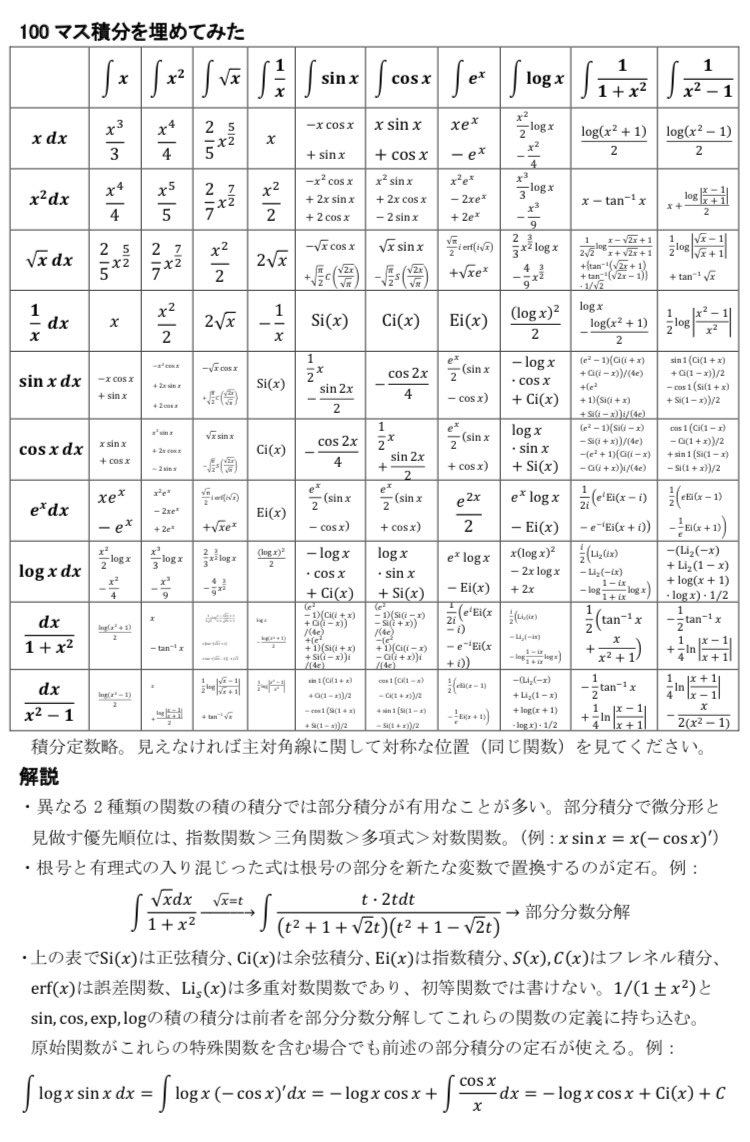
積分アレルギーのある人から「積分のチートばっかりだ」とクレームが入ったので積分と関係ないチートを考えました。
対称性・交代性を上手く使えば、面倒な文字式の計算を全くせずに因数分解できます。
対称性や交代性がない式の因数分解も多変数の因数定理で楽にできる場合もあります。
#チート式
87
位相が強まると、部分集合が開・閉になりやすくなり、稠密になりにくくなり、閉包が小さくなり、点列が収束しにくくなり、その空間を始域とする写像が連続になりやすくなり、終域とする写像が連続になりにくくなり、分離性が良くなり(従ってハウスドルフになりやすくなり)、コンパクト性が悪くなる。
88
89
数III以外のチートも見たいという意見が多かったので数IIのチートを考えました。
お題は記述でも堂々と使える二重接線を瞬時に求める式変形テクと、記述では使わない方がいいけど検算で役立つ1/30公式等の一般化。
受験期真っ只中でもきちんとTwitterを見ている良い子の皆さんへプレゼント!
#チート式
90
91
前回のチート式では「脱法ロピタル」が好評だったので「脱法パップスギュルダン」も作ってみました。記述も計算も楽です。この手法はあまり知られていないと思います。
重心の定義からパップスギュルダンの定理とほぼ等価ですが、有名な裏技であるバウムクーヘン積分はより広範に使えます。
#チート式
92
93
94
97
99
高校生は無意識に"原点を通らない"グラフを想像して「原点で0じゃない」という表現に違和感を覚えるみたいですが、大学で数学や物理を学んだ人は無意識に高次元への一般化を想像してx=0を実1次元空間ℝあるいは複素数平面ℂの原点だと思ってそこで関数値が0でないと考えるので自然に感じるらしいです。
100
ちなみに、私が以前やったtan治郎ネタはこのtan治郎平面です。
#tan治郎 twitter.com/keisankionwyki…