101
105
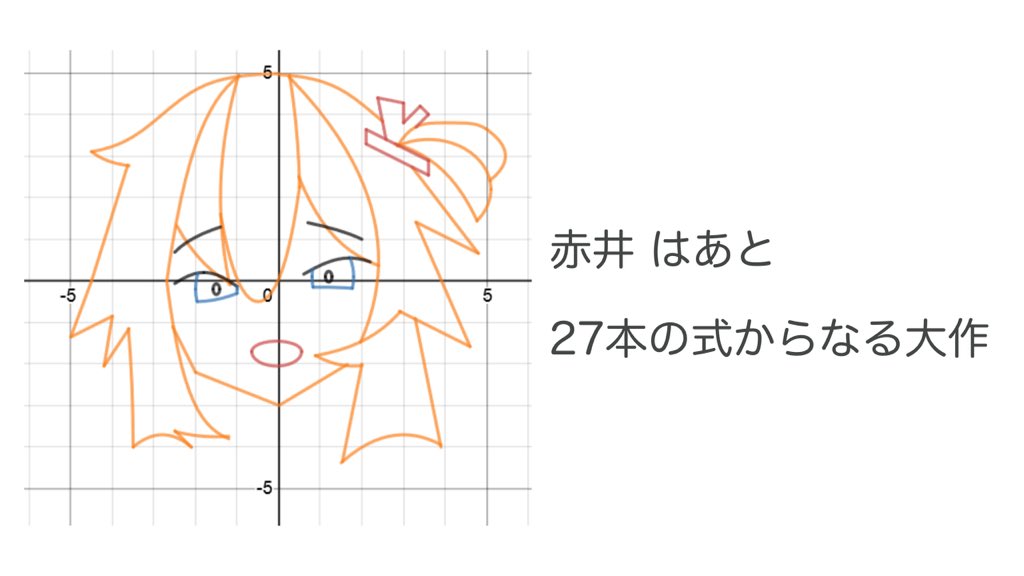
107
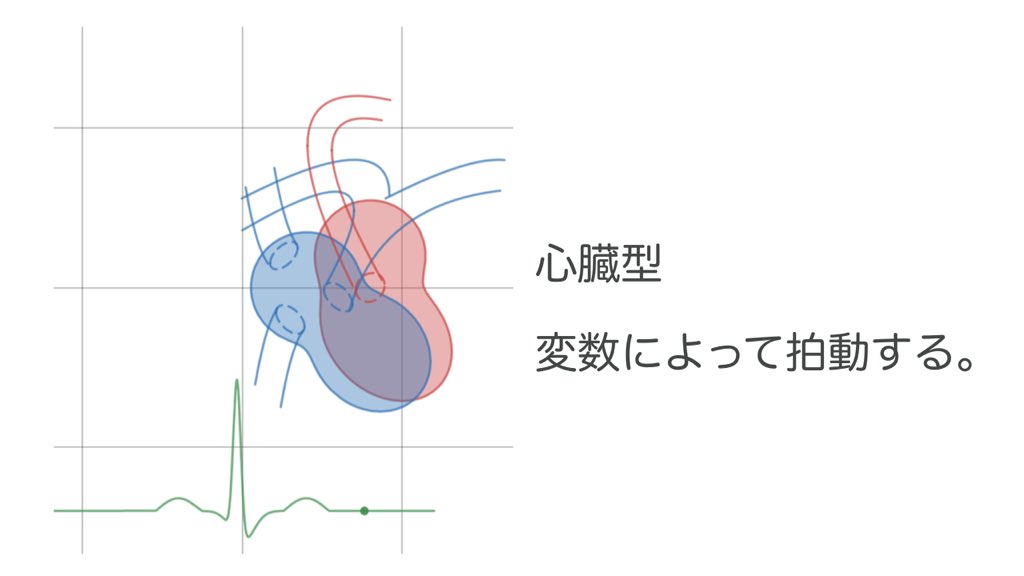
「黄金虚数」
#ますらば問題
108
今から4000年以上前、日本がまだ縄文時代だった頃にメソポタミア人たちは太陽の動きが約360日の周期を持っていることに気づきました。
1日に動く太陽の動きを観察するために円を360等分した角度を1°としたと言われています。
109
111
112
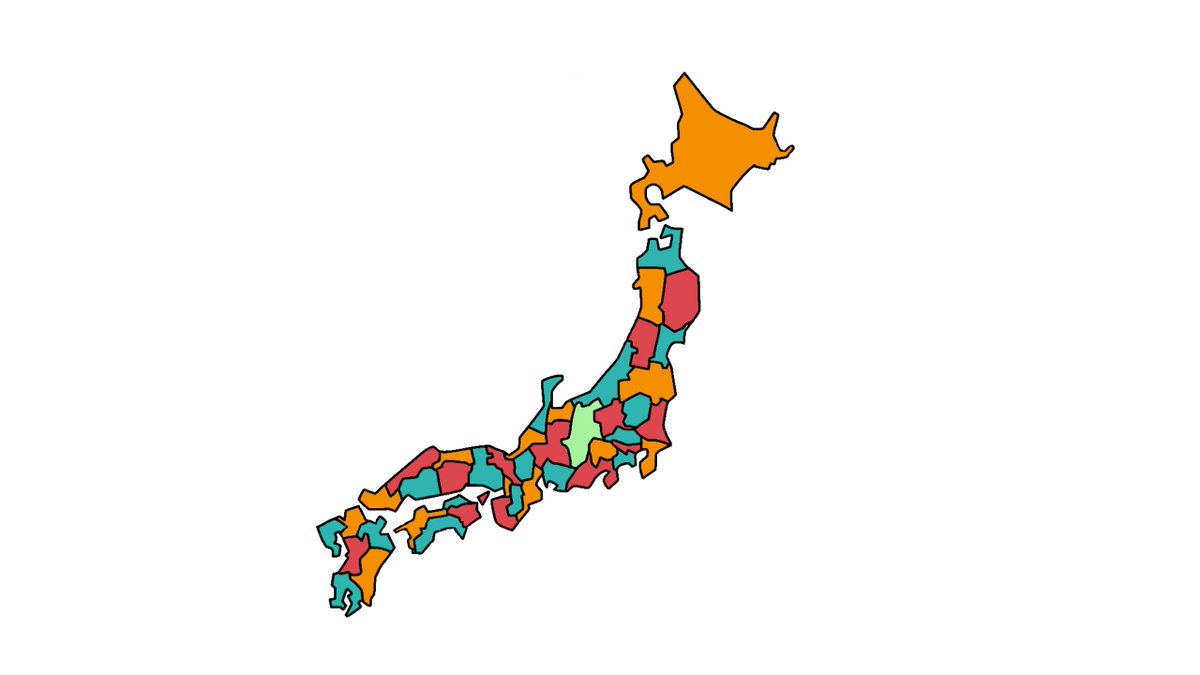
申し訳ございません。
フリーの白地図を用いたのですが、佐賀県と長崎県が合併されていることに気づきませんでした。
114
116
【1は素数か】
1は素数ではありませんが、1が素数だとすると
6=2×3=1×2×3=1×1×2×3
のように素因数分解に一意性がなくなってしまいます。
ルベーグは1を素数だと考えた最後の著名な数学者だといわれています。
118
【ゴールドバッハ予想】
「2より大きい全ての偶数は、2つの素数の和として表せる。」
この未解決問題を提示したクリスティアン・ゴールドバッハは、オイラーと同じ時代の数学者です。
現在では、4×10¹⁸まで正しいことが確認されていますが、完全な証明はなされていません。
#まいにち未解決問題
119
【双子素数は無数にあるのか】
(5,7),(11,13)など、差が2である2つの素数の組を双子素数といいます。双子素数は無限に存在するのか、未だわかっていません。
現在、差が246以下の素数の組が無数にあることは示されています。
この246を2に書き換えることが待望されています。
#まいにち未解決問題
121
【コラッツ予想】
「nが偶数ならば2で割る。」
「nが奇数ならば3倍して1を足す。」
任意の自然数はこの操作を有限回繰り返すと必ず1に到達するのか。
現在までに5×2⁶⁰以下で反例がないことが確かめられています。
これを解いた者には500ドルの賞金が与えられます。
#まいにち未解決問題
122
123
【ソファ問題】
「幅を1とするL字型通路を通り抜けることができる、ソファの面積の最大値を求めよ。」
レオ・モーザーが提示した未解決問題です。ソファは円でもいいし、正方形でもいいです。
ちなみに、『たけしのコマ大数学科』で取り上げられました。
#まいにち未解決問題