26
天文学者、物理学者、数学者がスコットランドの列車で外を眺めていた。
天文学者「この微分方程式の解が知りたいんだけど…」
物理学者「ああ、それならこうすれば解けるよ」
数学者「ちょっと待てそんな操作本当にしていいのか？」
羊（……誰か俺のこと見ろよ……）
27
数学徒「やった！すごい定理を見つけたぞ！」
湯婆婆「定理？贅沢な名だね。お前の見つけたものはただの系だよ！系！」
数学徒「系」
28
「九九の7の段が難しいんだよね」
「mod 7で考えると楽だよ」
「7×1≡0、7×2≡0、7×3≡0、7×4≡0…ほんとだ！！！！」
29
子ども「もしかして九九って右下と左上が同じなんじゃない？」
親「お！いいところに気づいたね！」
子ども「つまり整数の集合は積に関して可換モノイドになるわけか」
親「急にレベルが上がったな」
30
数学で使える接続語
「ゆえに」
「よって」
「したがって」
「このとき」
「すなわち」
「つまり」
「余白が狭すぎるため」
31
博士「苦節30年…ついに嘘発見器が完成したぞ！」
助手「流石です博士！」
博士「試しに何か言ってみたまえ！」
助手「『私は嘘をついています』」
博士「いきなり壊そうとするんじゃない」
32
大学数学を知らずに数学科に入った主人公が「お前、群も知らないのかよww」と周囲に馬鹿にされるも、実は線形代数だけを10年間勉強してきており、みんなが悩んでいる問題を「なんだ、ただの線形代数じゃん」と簡単に解いて無双する話「リニア・ビギナー」
33
Q. なぜ奇数の素数は無限にあるのに偶数の素数は2しかないのか
A. かつては2以外の素数もたくさんあったが、偶数は割れやすいため他の素数に捕食される場合が多く、1番小さい2だけが生き残った
34
問題「半径2の円の面積を求めなさい」
数学徒「簡単じゃん」
問題「ただし有効数字は62兆8000億桁とする」
35
男「あ、財布が落ちてる。どうしよう…」
天使「正直に交番に届けましょう。いいことをすれば気持ちがいいものです」
男「天使……」
悪魔「おいおい、それより俺とほとんど至る所の微分係数が0なのに0から1までの値を連続的にとる関数作ろうぜ」
男「カントールの悪魔……」
36
37
太郎さんと花子さんは15^20について話している。
太郎「15^20は何桁なんだろう？このまま求めるのは大変だからlogの値が上手く使えないかな？」
花子「そうかしら？15^20= 332525673007965087890625だから24桁じゃない？」
太郎「本当だ。やっぱりゴリゴリの計算力は何でも解決するんだね」
38
卒業式
女子「よかったらくれませんか？先輩の第二…」
先輩「ああ第二ボタンね。いいよ」
女子「第二象限！」
先輩「え！？」
瞬間、先輩の右上半身の自由が効かなくなる
先輩「こ、これは…」
その女子の数学固有スキル「奪象限」能力：相手の臍を原点と見なし１つの象限のコントロールを奪う
39
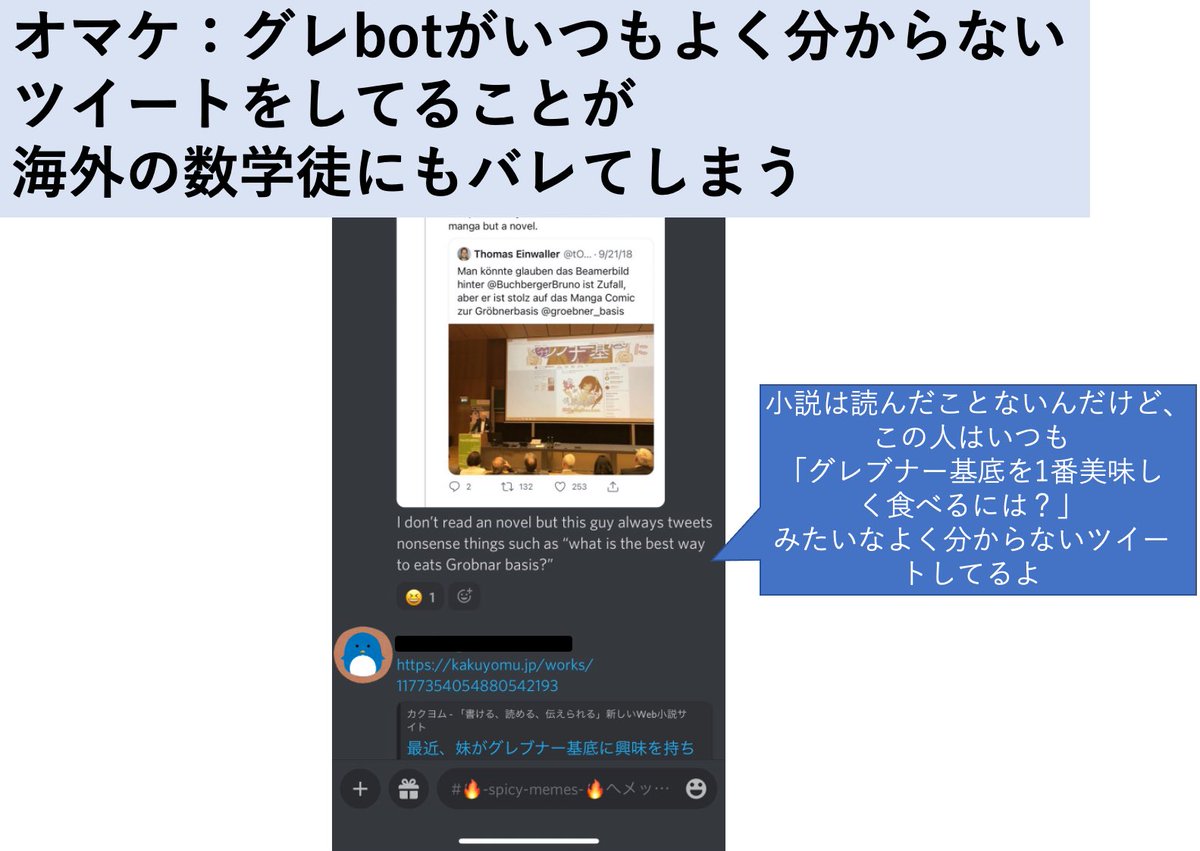
自分の書いた小説が東大の中間試験の参考文献に登場するという人生初の経験をしているぶな
三角関数禁止法 - カクヨム kakuyomu.jp/works/11773540… twitter.com/HamaguchiKoich…
40
なぜか海外の大学院生のDiscordで話題になったグレ妹の反応についてまとめたぶな
※日本語はグレbot 訳
※アイコンと名前は隠してます
41
教師「それじゃあ2人組作って〜」
生徒「先生！1人余ります」
教師「それじゃあ3人組作って〜」
生徒「それだと2人余ります」
教師「それじゃあ5人組は？」
生徒「その場合4人余りますね」
教師「クラスの人数が30人以下だとする時、中国剰余定理から人数を求めなさい」
43
10年後の僕「俺も昔は数学の概念にガチ恋してた時があってな～ｗ」
娘「えー、パパ気持ち悪い…」
僕「い、今はお前が一番大切だぞっ！」
娘「やった！でさ、パパがガチ恋してた概念って何なの？」
僕「それはな…」
グレブナー基底「ご飯たけたよぉ〜！！」
44
子ども「鬼はー外！福はーうち！」
鬼「じゃあ、次の集合Rは、Rの外かな内かな？」
R={X|X∉X}
子ども「えーと、R∉Rとすると、定義からR∈Rになって、逆にR∈RとするとR∉Rになって……あれ？」
鬼「今だ！混乱してるうちに家の中に侵入しろっ！！」
45
子ども「ねーねー、もしかして”九九”って『みぎうえ』と『ひだりした』のかずが、おなじなんじゃない？」
親「お！いいところに気づいたね〜！実は3×4と4×3は同じ数なんだよ〜」
子ども「へー、つまり自然数全体の集合は積に関して可換モノイドになるわけか」
親「理解力ありすぎるだろ」
46
アニメ「数学科」
第1話「線形代数」
第2話「群論」
第3話「線形代数」
第4話「環論」
第5話「線形代数」
第6話「体論」
第7話「線形代数」
第8話「表現論」
第9話「線形代数」
第10話「線形代数」
第11話「線形代数」
最終話「線形代数」
47
数学書「理解できなかったら購入代金を全額お返しします！」
数学徒「まじか。返金してもらお」
著者「どこが分からなかったですか？」
数学徒「この部分ですね」
著者「ここは代数閉体の性質を使っていて〜」
数学徒「あー、なるほど！」
数学徒「くそ！今日も返金してもらえなかった！」
コンピュータを使った数学を研究している研究者。趣味で小説も書いてました。代表作「妹がグレブナー基底に興味を持ち始めたのだが。」bit.ly/2ZbpP7W /Web作家経歴：peep公式作家、CHAT NOVEL公式作家/受賞歴:カクヨムWeb小説短編賞受賞（漫画化）