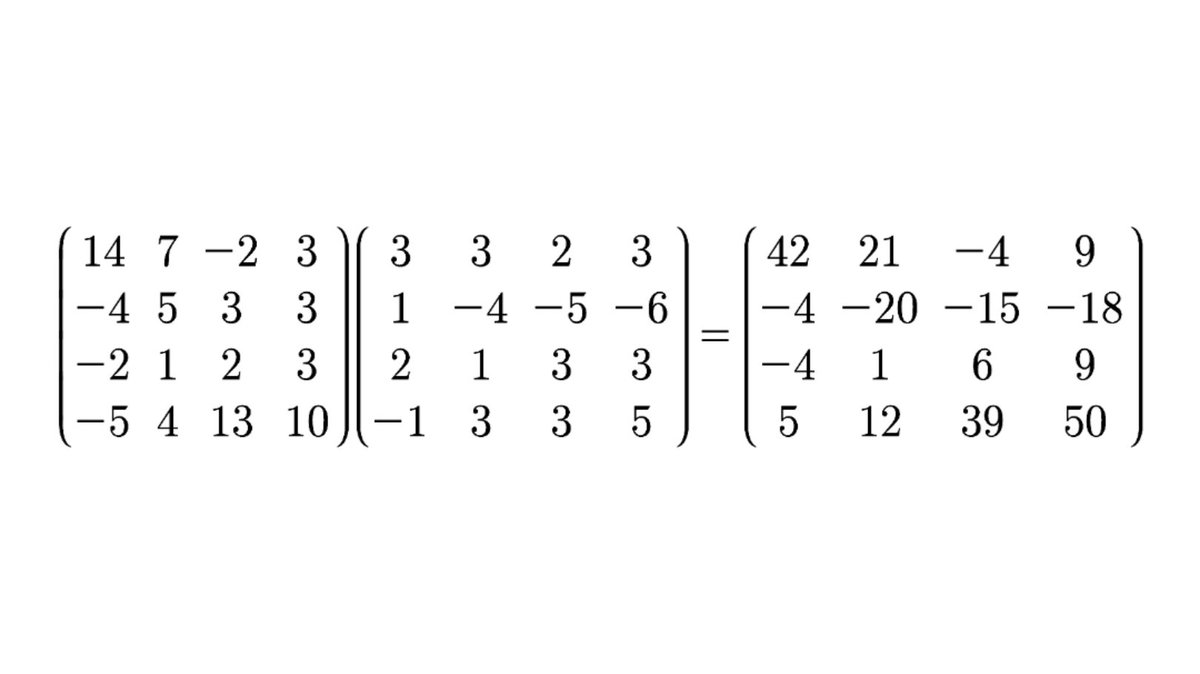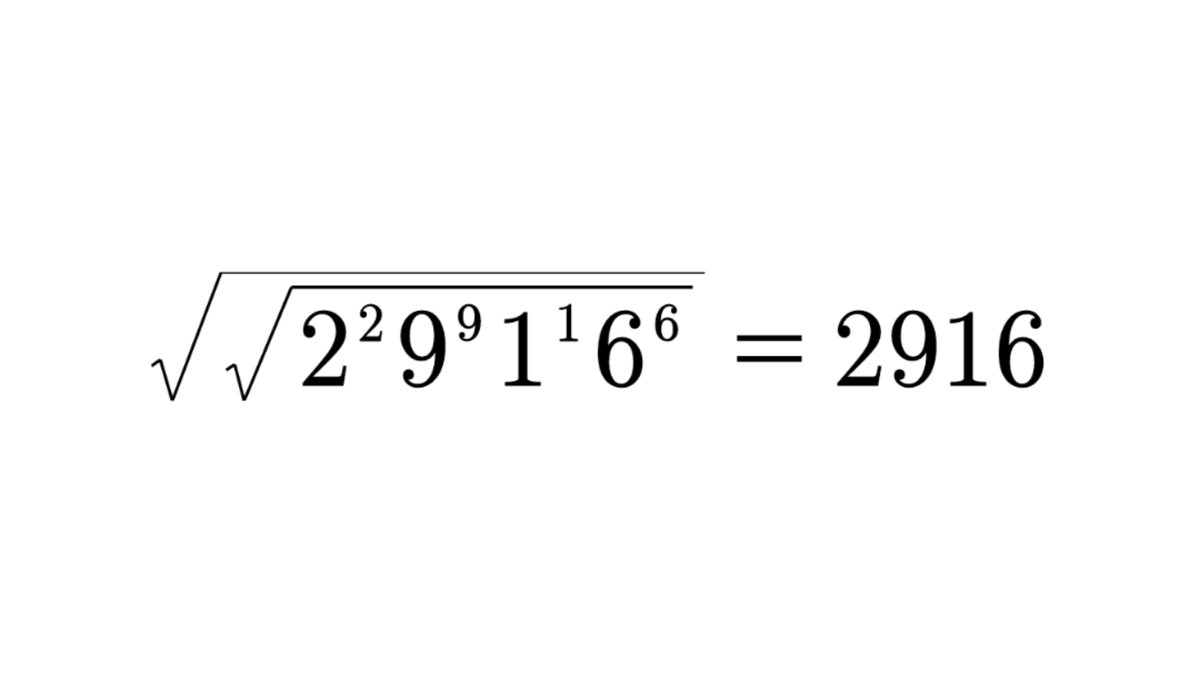78
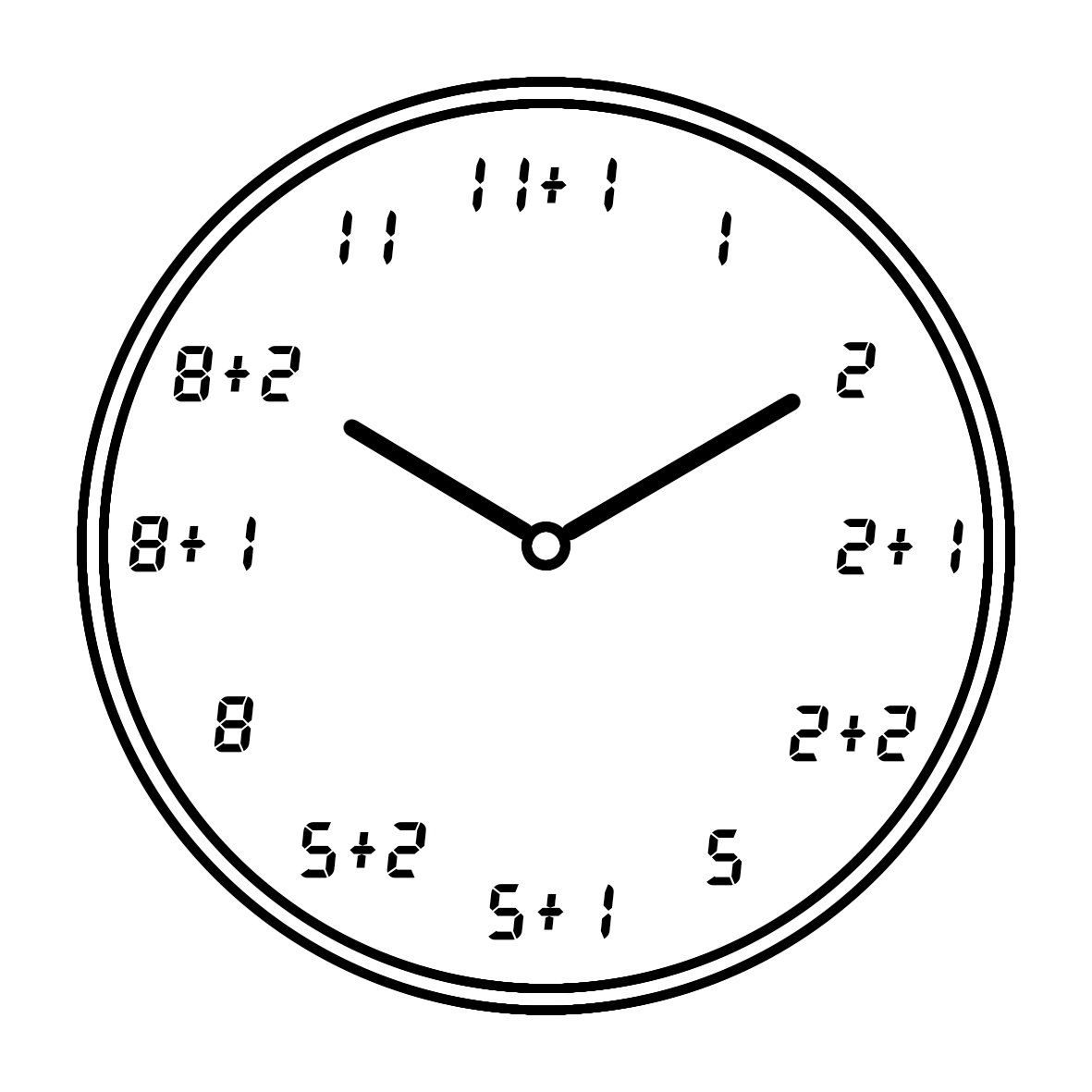
第2回「一種類の数字でどれだけ美しい等式作れるか選手権」を開催します。
81
82
え、え、え、!
こんなシンプルな1つの図形で、非周期に平面を充填できるんですか!?衝撃的です!! twitter.com/cs_kaplan/stat…
84
87
【WANTED/Collatz problem】
数学の有名な未解決問題である『コラッツ予想』に、2021年7月7日、懸賞金1億2000万円がかけられました。これは、数学史上最高額の懸賞金となるそうです。コラッツ予想の内容は簡単に理解できるものです。数学自慢の方々、是非挑戦してみませんか。
mathprize.net/ja/posts/colla…
89
@bozu_108 小学生の夢を叶えました!
90
【#ほとんど正三角形】
方眼紙にかける簡単かつ高精度な、ほとんど正三角形を考えました。4×4でかけます。これは自信作です!
95
『円周率に終わりがない理由を一般向けに説明しよう選手権』を開催します!
99
つまり、図形問題は三角関数を使わずにすべて初等幾何で解こうってこと?