51
(x²+y²−1)³=x²y³
どんな形のグラフになる?(再)
53
「めっちゃ素数っぽいけど合成数」選手権を開催します!
54
外角の和は360°(再)
55
私からも1つ。
錘体の体積は柱体の体積の1/3であることを視覚的に理解する助けとなるように、10年ほど昔に作りました。思いついた当時はオリジナルだと思っていて自信作のつもりでしたが、後に有名だと知って残念に思ったことを覚えています。
56
「1から9までの数字を1回ずつ使った美しい等式選手権」手抜いたで賞
twitter.com/kaz49902036/st…
57
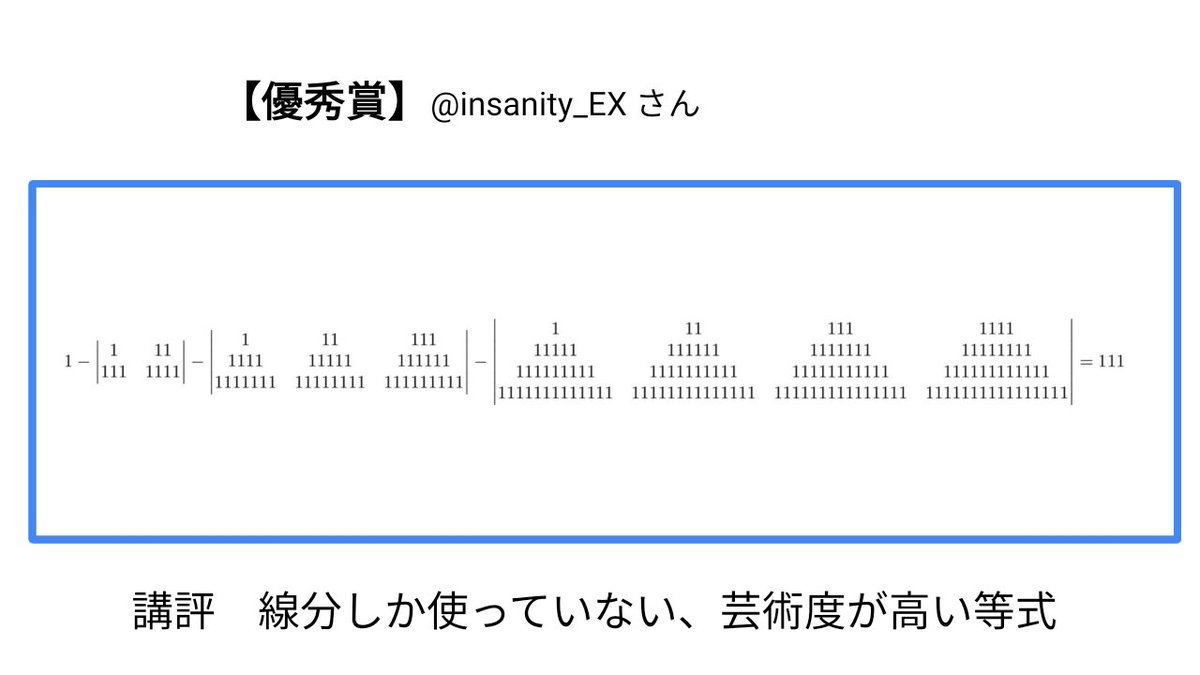
「1から9までの数字を1回ずつ使った美しい等式選手権」最優秀賞 twitter.com/jox_com_math/s…
58
【話題】
中学1年生が
「数学をなんで学ばなくてはいけないの?いつ役に立つの?」
と聞いてきました。
納得できる回答をお願いします!
59
【話題】
素人質問で恐縮ですが、分数のわり算は、何故ひっくり返して掛けるのでしょうか?
60
【話題】
中学1年生が、
『(負の数)×(負の数)=(正の数)』
になる理由がわからなくて困っています。わかりやすい説明をお願いします!
61
@bozu_108 適当と適当
63
第2回「一種類の数字でどれだけ美しい等式作れるか選手権」を開催します。
66
令和2²年2²月2²日2²時2²分2²秒!
70
ついに、見つけました! twitter.com/potetoichiro/s…
71
@Soviet_Usako 西暦13446204年には、素数の日がない。
134462040101...素数じゃない
134462040102...素数じゃない
⋮
134462041230...素数じゃない
134462041231...素数じゃない
72
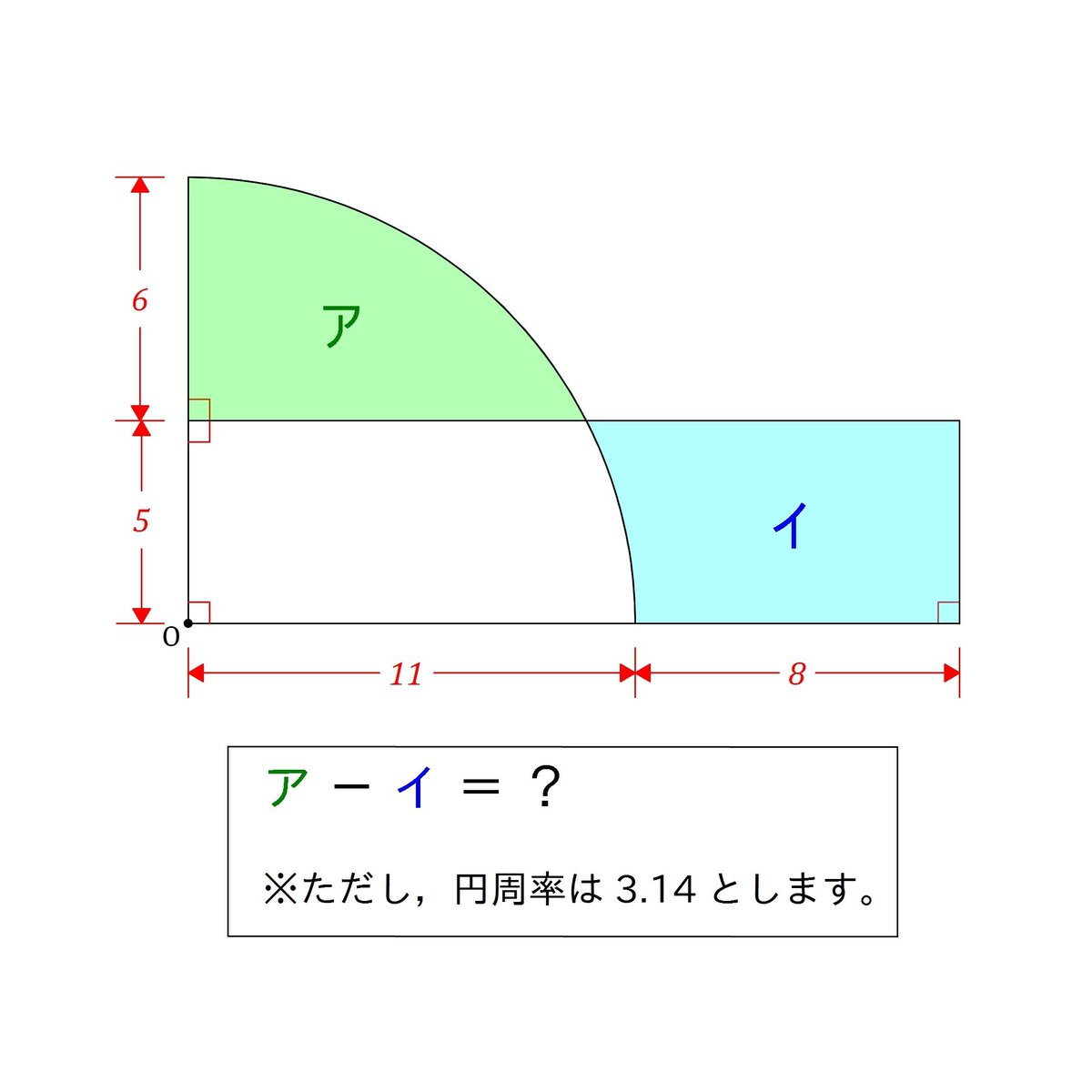
3月14日なので、3.14で計算して下さい!#円周率の日
73
【円周率(再)】#円周率の日
A「円周率どこまで覚えてる?」
B「それなりに覚えてるよ。Aは?」
A「14159265までだよ。Bは?」
B「僕はもう少し覚えてるよ」
A「次なんだっけ?」
B「7968195888だよ。8が3つ並ぶから覚えやすいよ」
A「ありがとう。覚えてみるよ」